ASME B31G. Failure pressure of the corroded pipe (original)

Calculate failure pressure of the corroded pipe according to Original B31G, Level-1 algorithm listed in ASME B31G-2012.

The next assumption of the corrosion shape is adopted by ASME B31G-2012:

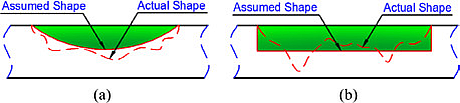
There (a) is a parabolic and (b) is a rectangular idealizations of a corroded area.

Usage

b31gpf(d, wth, smys, depth, l)

Arguments

d

nominal outside diameter of pipe, [inch]. Type: assert_double.

wth

nominal wall thickness of pipe, [inch]. Type: assert_double.

smys

specified minimum yield of stress (SMYS) as a characteristics of steel strength, [PSI]. Type: assert_double.

depth

measured maximum depth of the corroded area, [inch]. Type: assert_double.

l

measured maximum longitudinal length of corroded area, [inch]. Type: assert_double.

Value

Estimated failure pressure of the corroded pipe, [PSI]. Type: assert_double.

Details

Since the definition of flow stress, Sflow, in ASME B31G-2012 is recommended with Level 1 as follows:

$$S_{\text{flow}} = 1.1\cdot\text{SMYS}$$

no other possibilities of its evaluation are incorporated.

For this code we avoid possible semantic optimization to preserve readability and correlation with original text description in ASME B31G-2012. At the same time source code for estimated failure pressure preserves maximum affinity with its semantic description in ASME B31G-2012 and slightly differs from that given by Timashev et al. The latter deviates up to 0.7 % on examples supplied with CRVL.BAS - (b31gdata).

Numeric NAs may appear in case prescribed conditions of use are offended.

References

1. ASME B31G-2012. Manual for determining the remaining strength of corroded pipelines: supplement to B31 Code for pressure piping.

2. S. Timashev and A. Bushinskaya, Diagnostics and Reliability of Pipeline Systems, Topics in Safety, Risk, Reliability and Quality 30, doi:10.1007/978-3-319-25307-7 .

See also

Other Failure estimation: b31gmodpf(), dnvpf(), mepof(), pcorrcpf(), shell92pf()

Examples

library(pipenostics)

## Example: maximum percentage disparity of original B31G
## algorithm and modified B31G showed on CRVL.BAS data
with(b31gdata, {
  original  <- b31gpf(d, wth, smys, depth, l)
  modified  <- b31gmodpf(d, wth, smys, depth, l)
  round(max(100 * abs(1 - original / modified), na.rm = TRUE), 4)
})
#> [1] 32.6666

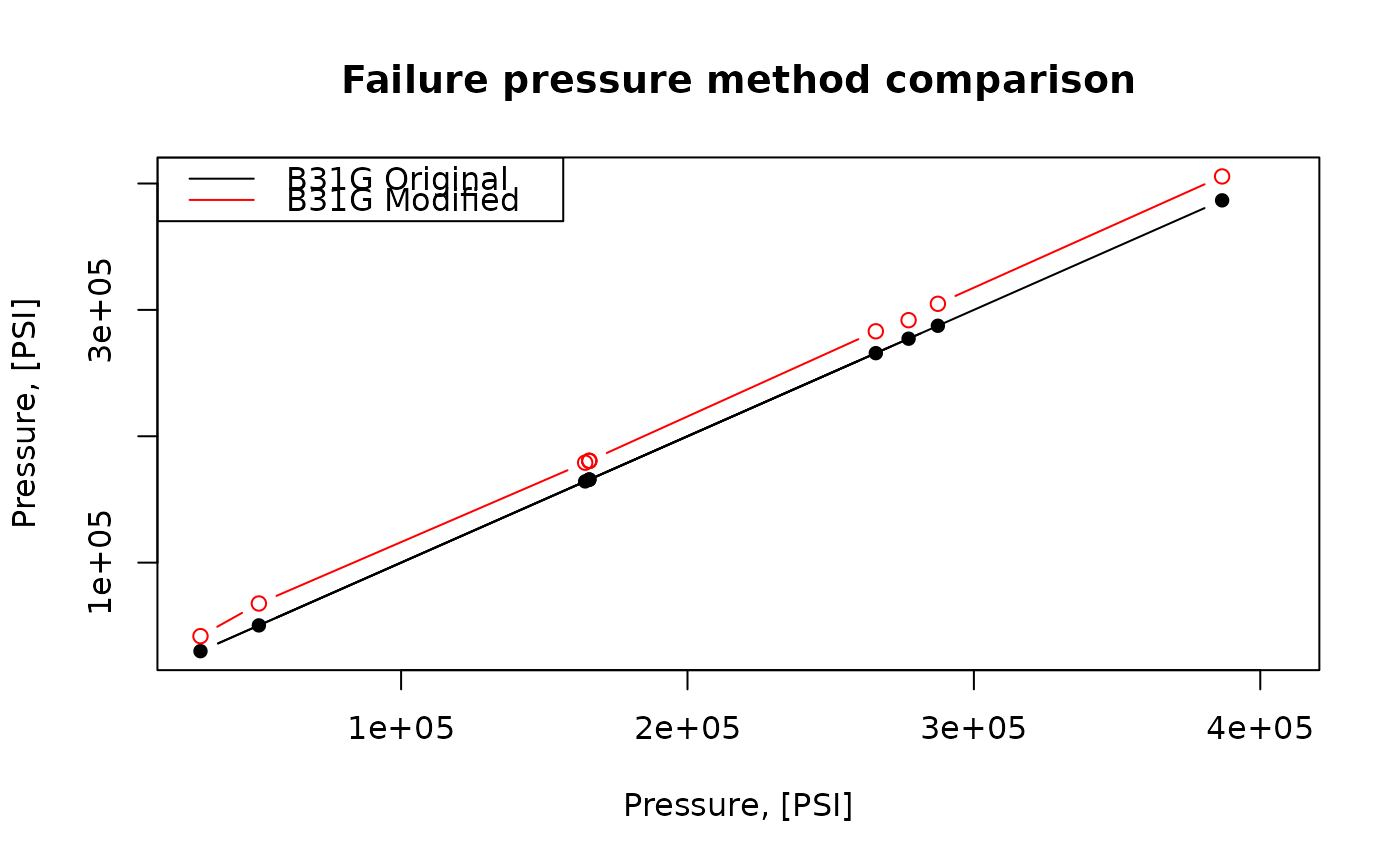
## Example: plot disparity of original B31G algorithm and
## modified B31G showed on CRVL data
with(b31gdata[-(6:7),], {
  b31g  <- b31gpf(d, wth, smys, depth, l)
  b31gmod  <- b31gmodpf(d, wth, smys, depth, l)
  axe_range <- range(c(b31g, b31gmod))
  plot(b31g, b31g, type = 'b', pch = 16,
       xlab = 'Pressure, [PSI]',
       ylab = 'Pressure, [PSI]',
       main = 'Failure pressure method comparison',
       xlim = axe_range, ylim = axe_range)
  inc <- order(b31g)
  lines(b31g[inc], b31gmod[inc], type = 'b', col = 'red')
  legend('topleft',
         legend = c('B31G Original',
                    'B31G Modified'),
         col = c('black', 'red'),
         lty = 'solid')
})